Modelling scenarios of the epidemic of COVID-19 in Canada
This paper (with plain-language summary) describes predictive modelling of COVID-19 in general, and efforts within the Public Health Agency of Canada to model the effects of non-pharmaceutical interventions (NPIs) on the transmission of SARS-CoV-2 in the Canadian population to support public health decisions. The article describes and uses a deterministic model, developed in Analytica software as the basis to provide a synopsis of results related to various NPIs. Finally, hospitalization and death rates are assessed using different scenarios for the total number of people infected with COVID-19 in Canada.
Download the full article summary here.
Glossary of Terms
COVID-19 Modelling Glossary of Terms
Using and Understanding the Mathematical Model
1. To view and run this file, you will need the free version of Analytica, available here.
2. After downloading Analytica, download the following file:
PHAC Modelling Code for Analytica
The file should automatically open with Analytica. But, if you run into any issues, the following tutorial explains how to open files using the software: To Open or Exit a Model.
3. Download the PHAC instruction guide:
Instructions for Using the COVID-19 PHAC SEIR Compartmental Model
Model Summary and Webinar
Transcripts:
Mathematical modelling of infectious diseases is primarily intended to study the spread and the duration of an epidemic, understand the magnitude of the challenge posed by the disease and the potential impact of interventions. Modelling allows public health decision-makers to work with provincial, territorial and international partners to base their responses to epidemics on the latest science and situational assessment. Modelling also forecasts the possible future spread of disease in Canada, and estimates a range of possible numbers of cases, hospitalizations, and deaths that may occur.
One of the models developed by The Public Health Agency of Canada (PHAC) for the transmission of severe acute respiratory syndrome virus 2 (SARS-COV-2) – the agent of the coronavirus disease 2019 (COVID-19) – is a compartmental model developed using Analytica software¹. The model is a dynamic Susceptible-Exposed-Infectious-Removed (SEIR) model that uses differential equations to estimate the change in populations in the various compartments. These compartments are connected between each other and individuals can move from one compartment to another, in a specific order that follows the natural infectious process. The model uses knowledge obtained from studies around the world on the biology of transmission of the virus causing COVID-19 to produce a mathematical representation of how COVID-19 may spread in the Canadian population under different scenarios.
In a Susceptible-Exposed-Infectious Removed (SEIR model):
Susceptible (S) individuals have never been infected by the pathogen and therefore can become infected.
Exposed (E) individuals have been infected with a pathogen, but they are not yet infectious, because of the latent period of the disease.
Infectious (I) individuals are infected and are able to transmit the pathogen to others.
Removed (R) individuals are no longer able to transmit the disease. This group includes the recovered individuals and the fatalities.
The logic, assumptions and structure of the model are summarized and illustrated in Figure 1. Since this virus is one that humans have never been exposed to before, the basic assumption is that the entire population starts in the Susceptible compartment. The initial condition is such that infectious individuals are introduced into the population and this “seeds” the epidemic. Contact rates between individuals combined with the number of infectious and susceptible individuals in the population, are used to calculate the probability that a susceptible person and an infectious person come into contact within a finite time period. This probability is then combined with the probability that the contact got infected, to estimate the rate at which susceptible individuals move into the exposed compartment.
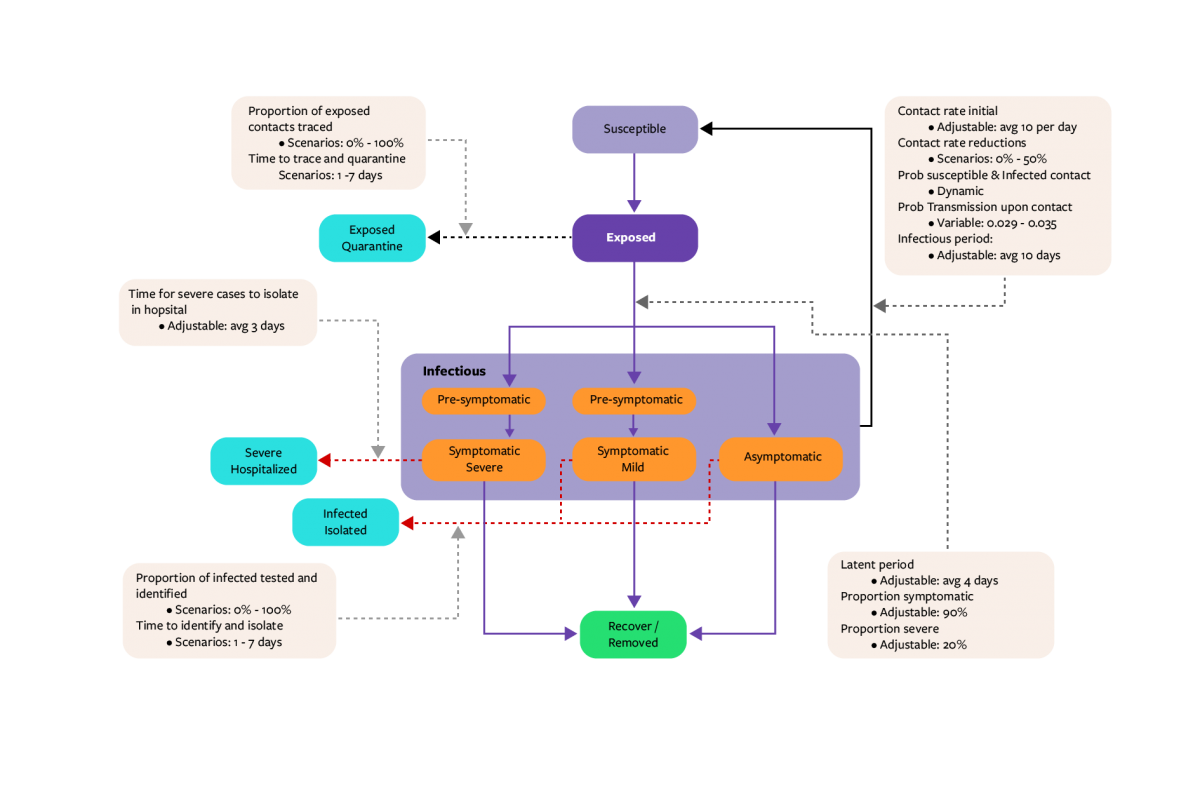
Subsequently, progression of individuals in the model from the exposed model compartment into the infectious severe, infectious mild or infectious asymptomatic stages is dictated by both the latent period and the proportion of people estimated to be asymptomatic, severe or mild. The estimates are derived from studies in different countries already experiencing the epidemic. The infectious period then dictates the rate at which the infectious population progresses to the recovered/removed compartment. A key assumption at this stage is that the population remains immune from further infection for the duration of the time period modelled.
Key factors that modify the rate of transmission and the ultimate outcomes predicted by the model include:
- Physical distancing effects having an impact on contact rates,
- Exposed individuals being quarantined as a result of contact tracing,
- Severely symptomatic infectious individuals getting hospitalized and, as a result, being isolated and no longer spreading infection in the community, and
- Mildly symptomatic and asymptomatic individuals being isolated as a result of enhanced testing in the community.
The model uses best estimates for some parameters, which can be replaced with probability distributions (a range) to reflect uncertainty. In addition, the model naturally allows for parametric analysis to be done when a range of parameter values are used prior to viewing the results.
